4763. От списка рёбер к матрице
смежности
Простой
неориентированный граф задан списком рёбер. Выведите его представление в виде
матрицы смежности.
Вход. В
первой строке заданы два целых числа n
(1 ≤ n ≤ 100) – число
вершин и m (1 ≤ m ≤ n · (n – 1) / 2) – число
рёбер. Далее в m строках содержаться m пар чисел, каждая из которых описывает
одно ребро графа.
Выход. Выведите
матрицу смежности графа.
|
Пример входа |
Пример выхода |
|
3 3 1 2 2 3 1 3 |
0 1 1 1 0 1 1 1 0 |
РЕШЕНИЕ
графы
Анализ алгоритма
Читаем ребра, строим матрицу смежности неориентированного
графа. Затем выводим ее.
Пример
Граф, заданный в
примере, имеет вид:
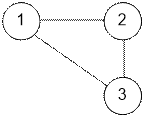
Реализация
алгоритма
Объявим матрицу смежности g.
#define MAX 110
int
g[MAX][MAX];
Читаем матрицу смежности. Для каждого ребра графа (a, b)
устанавливаем g[a][b] = g[b][a] = 1.
scanf("%d %d",&n,&m);
memset(g,0,sizeof(g));
for(i
= 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
g[a][b] = g[b][a] = 1;
}
Выводим матрицу смежности графа.
for(i
= 1; i <= n; i++)
{
for(j = 1; j
<= n; j++)
printf("%d
",g[i][j]);
printf("\n");
}
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int g[][] = new int[n+1][n+1];
for(int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
System.out.print(g[i][j] + " ");
System.out.println();
}
con.close();
}
}